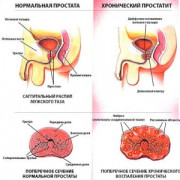
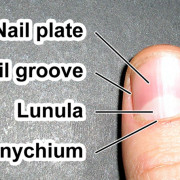
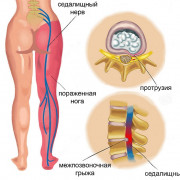
Самое актуальное и обсуждаемое
Популярное
Полезные советы
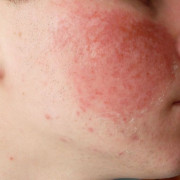
Важно знать!
10 лучших таблеток от прыщей
Особенности препаратов
Лекарства, которые направлены на борьбу с акне, или же другими формами прыщей действуют в зависимости от состава.
Препараты действуют, таким образом, на кожные покровы человека:
их...
Читать далее
13 неделя беременности
14 приемов, чтобы определить беременность без теста: народные методы в домашних условиях
5 симптомов рака анального канала, о которых вы должны знать
3 способа вылечить генитальный герпес у женщин, как он выглядит, можно ли заниматься сексом
5 полезных свойств зеленой гречки для здоровья по мнению ученых
9 причин возникновения белых точек на ногтях
37 неделя беременности
15 симптомов почечного давления. причины и лечение
9 неделя беременности (1 триместр)
Рекомендуем
Лучшее

Важно знать!
6 акушерская неделя беременности: ощущения в животе
Как меняется ребенок?
Развитие плода продолжается в интенсивном темпе. На данном этапе все больше дифференцируются внутренние органы. Главными изменениями остаются:
Практически окончательное деление главного...
Читать далее
21 неделя беременности: что происходит с малышом и мамой, фото, развитие плода
2 самых эффективных аппарата для проверки зрения: как можно увидеть глаз изнутри?
5 ступенчатая терапия бронхиальной астмы с препаратами
7 неделя беременности: что происходит с плодом и мамой
10 правил женской гигиены, о которых вы должны знать
36 неделя беременности
36 неделя беременности: что происходит на этой неделе?
12 признаков, что смерть уже рядом
21 причина изменения уровня альфа-фетопротеина в крови
Новое
Обсуждаемое

Важно знать!
5 антидепрессантов группы сиозс
Классификация антидепрессантов
Депрессии известны человечеству с незапамятных времен, как и способы их преодоления. В Древнем Риме известный лекарь Соран Эфесский применял для их лечения соли лития,...
Читать далее
10 лучших ноотропов
6 интересных фактов про дентин зуба
32 неделя беременности
20–22 день цикла: можно ли ощутить первые признаки беременности?
30 удивительных фактов о мозге и мышлении, которые заставляют призадуматься
7 лучших противовирусных средств
10 лучших успокоительных для детей
7 поз йоги, которые помогут избавиться от запора
15 лучших средств от простуды
Популярное
Актуальное

Важно знать!
7 популярных видов массажа
Спортивный массаж
Он просто необходим перед важными тренировками, а также при участии спортсменов в соревнованиях. Большинство травм происходит из-за неправильной разработки мышц. Частично с этой задачей...
Читать далее
28 неделя беременности
101 интересный факт о пуповине
10 безопасных способов, как вытащить клеща из тела человека в домашних условиях
10 страшных заболеваний, которые передаются по наследству
9 побочных эффектов избыточного употребления чая
6 признаков инсульта у женщин: первые симптомы
12 лучших пивных дрожжей
23 неделя беременности
10 лучших антигистаминных средств для детей
Обновления
 Статьи
Виниры: виды, методы установки, преимущества без обточки зубов
Статьи
Виниры: виды, методы установки, преимущества без обточки зубов
Виниры: виды, методы установки и особенности без обточки зубов - полный гид
В мире современной стоматологии...
 Здоровье
Уровень сахара в крови: факторы влияния и методы контроля для здорового образа жизни
Здоровье
Уровень сахара в крови: факторы влияния и методы контроля для здорового образа жизни
Как контролировать уровень сахара в крови
В современном мире забота о здоровье становится все более...
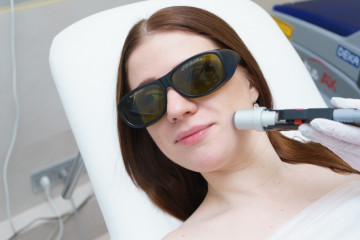 Статьи
Особенности ухода за кожей после лазерной эпиляции
Статьи
Особенности ухода за кожей после лазерной эпиляции
Лазерная эпиляция https://www.krasotamed.ru/uslugi/lazernaya-epilyatsiya/ - эффективный метод удаления...
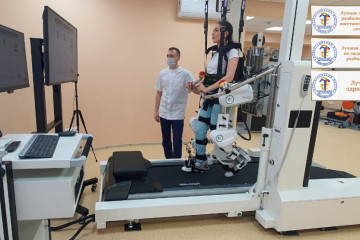 Здоровье
Заболевания опорно-двигательного аппарата: симптомы и лечение для поддержания здоровья.
Здоровье
Заболевания опорно-двигательного аппарата: симптомы и лечение для поддержания здоровья.
В мире современной медицины забота о здоровье опорно-двигательного аппарата становится важнее прежде,...
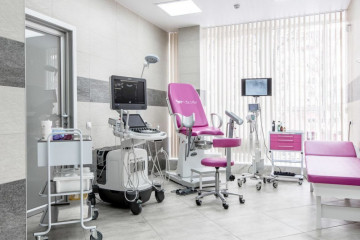 Беременность
Комфорт и безопасность: идеальный кабинет гинеколога для женского здоровья.
Беременность
Комфорт и безопасность: идеальный кабинет гинеколога для женского здоровья.
Идеальный кабинет гинеколога: Обеспечиваем комфорт и безопасность для женщин
В мире современной медицины,...
 Статьи
Фетальный кардиомонитор: мониторинг при беременности
Статьи
Фетальный кардиомонитор: мониторинг при беременности
Мониторинг плода
Кардиотокограф (КТГ) необходим для точного обследования матери и плода в кабинетах...
 Статьи
Дом для пожилых с плюсами: комфорт и забота для родственников
Статьи
Дом для пожилых с плюсами: комфорт и забота для родственников
Дом для пожилых людей - это не только место предоставления качественного ухода и безопасности для старшего...
 Статьи
Как выбрать метод лечения алкоголизма
Статьи
Как выбрать метод лечения алкоголизма
В современном мире существует множество методов лечения алкоголизма, начиная от медикаментозной терапии...
 Статьи
Правила и способы утилизации отходов в россии и мире
Статьи
Правила и способы утилизации отходов в россии и мире
Оборудование для сортировки мусора
Мусоросортировочные линии представляют собой конвейер. Они состоят...
 Статьи
Витилиго: другое аутоиммунное заболевание
Статьи
Витилиго: другое аутоиммунное заболевание
Витилиго — кожное заболевание, вызванное удалением меланоцитов или пигментных клеток. Когда это происходит,...
 Статьи
20 лучших брендов профессиональных кроссовок для бега
Статьи
20 лучших брендов профессиональных кроссовок для бега
Какие спортивные кроссовки лучше купить: критерии выбора
При выборе моделей важно обладать знаниями...
 Статьи
Педиатр кто это такой, особенности профессии, чем занимается, что лечит
Статьи
Педиатр кто это такой, особенности профессии, чем занимается, что лечит
Общие сведения
Педиатрия – обширная область медицины, которая занимается изучением физиологических...